用GNU Octave做优化
其实是初中数学的内容。
看研究高斯软件的并行效率时,作者根据公式
$ s = n \times (1.015 - n \times 0.0067) $
得出了「并行核数大概在75的时候达到最大速度」。我突然有点糊涂了,这个结论是怎么得出的呢?
明显这是一个初中数学问题,因为函数是个一元二次函数,有公式,可惜我已经忘光光了。用数形结合的思路
1 | f = @(x) -0.0067 * x.^2 + 1.015 * x; |
.png)
可以看出大概是75的时候效率最大,这时我也大概想起了公式是啥样的。不行,这个问题要一般话,要用专门的工具解决:
1 | phi = @(x) 0.0067 * x^2 - 1.01 * x; |
这里用Octave的sqp()函数求了phi()的最小值,这个phi()就是上面公式的值乘以−1,也就是把求最大值转换为求最小值,其他的量都默认,从1开始找最小值,求得的结果是75.373。
又是一次脱裤子放屁的经历。收获是又玩了一把Octave,但这个方法的价值不局限在这里,因为如果函数更为复杂,没有公式,图形又不好看,还需要精确求解的时候,该方法的优势就体现出来了。
举个栗子,某种药物的释放程度随时间变化,t分钟时释放比例以P表示,得到的数据是
1 | t = [0 2 4 6 8 10 15 17.5 22 30 45 60]; |
如果以如下的模型来拟合这些数据
$ P = 1 - e^{-K \times t} $
看不出来了吧,我可以拟合
1 | phi = @(K) abs(sum(P) - sum(1 - exp(-K * t))); sqp([0.01], phi) |
结果是0.11390,画图
1 | plot(t, P * 100, '@'); |
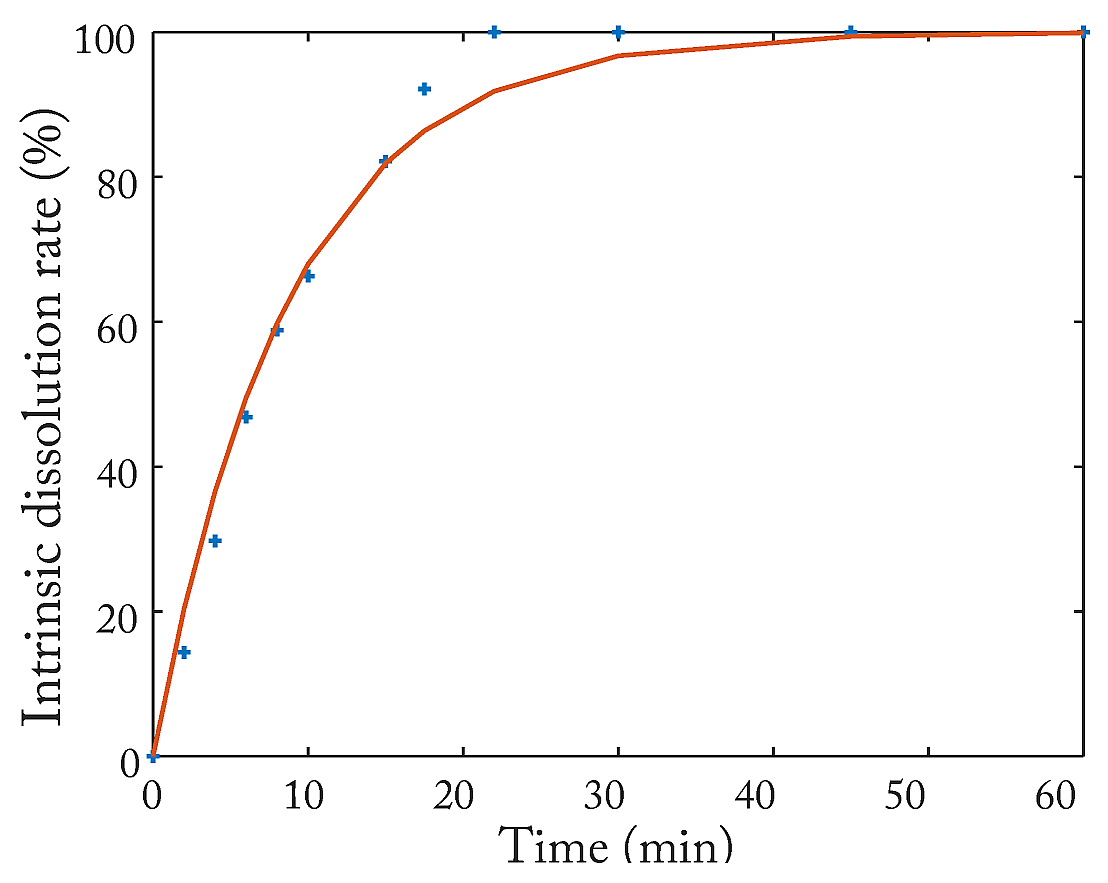
这两个图都用了一些技巧,除了坐标的位置动过外,还改了PostScript文件,怎么改另写一篇文章介绍咯。
2019-01-18 Update:
除了上面说的方法外,还可以用optim包里的函数进行优化:
1 | t = [0 1 3 5 10 15 20]; |
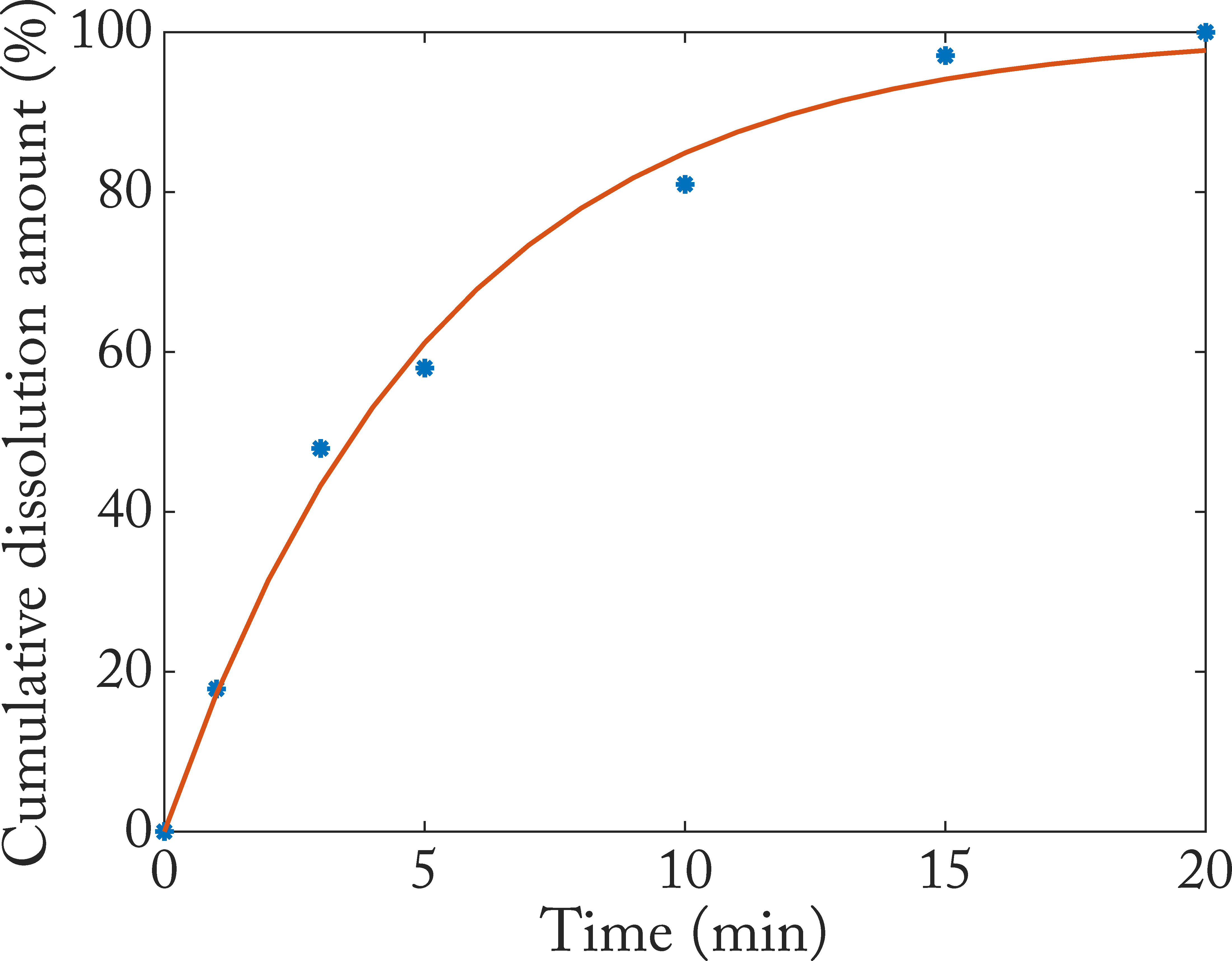
2019-07-05 Update:
补一个做logistic拟合的代码。
1 | data = [ |
2025-03-17 Update:
https://docs.octave.org/latest/Polynomial-Interpolation.html
再玩一下酒精浓度和密度的关系,数据从国标抄的。
1 | alc = [ |
$\rho = -7.0783 \times 10^{-8} \times Vol%^5 + 1.8019 \times 10^-5 \times Vol%^4 - 1.7055 \times 10^{-3} \times Vol%^3 + 5.8862 \times 10^{-2} \times Vol%^2 - 1.8559 \times Vol%^1 + 9.9838 \times 10^2$
或者您可以把评论发在别处,添加指向本页的连接,然后把网址告诉我:
本文标题:用GNU Octave做优化
文章作者:Chris
发布时间:2017-03-26
最后更新:2025-03-17
原始链接:https://chriszheng.science/2017/03/26/Optimization-using-GNU-Octave/
版权声明:本博客所有文章除特别声明外,均采用 CC BY 4.0 许可协议。转载请注明出处!
分享